Documents (examples.documents)

In this example of text analysis we consider the text processing application inspired by [Albright2006].

We used the Medlars data set, which is a collection of 1033 medical abstracts. For example we performed factorization on term-by-document matrix by constructing a matrix of shape 4765 (terms) x 1033 (documents). Original number of terms is 16017, the reduced number is a result of text preprocessing, namely removing stop words, too short words, words that appear 2 times or less in the corpus and words that appear 50 times or more.

Note

Medlars data set of medical abstracts used in this example is not included in the datasets and need to be downloaded. Download links are listed in the datasets. Download compressed version of document text. To run the example, the extracted Medlars data set must exist in the Medlars directory under datasets.

Example of medical abstract:

autolysis of bacillus subtilis by glucose depletion .                   
in cultures in minimal medium, rapid lysis of cells of bacillus       
subtilis was observed as soon as the carbon source, e.g. glucose, had   
been completely consumed . the cells died and ultraviolet-absorbing     
material was excreted in the medium . the results suggest that the cells
lyse because of the presence of autolytic enzymes . in the presence of  
glucose the damage to the cell wall caused by these enzymes is repaired 
immediately . 

Because of the nature of analysis, the resulting data matrix is very sparse. Therefore we use scipy.sparse matrix formats in factorization. This results in lower space consumption. Using, Standard NMF - Divergence, fitted factorization model is sparse as well, according to [Hoyer2004] measure of sparseness, the basis matrix has sparseness of 0.641 and the mixture matrix 0.863.

Note

This sparseness measure quantifies how much energy of a vector is packed into only few components. The sparseness of a vector is a real number in [0, 1]. Sparser vector has value closer to 1. The measure is 1 iff vector contains single nonzero component and the measure is equal to 0 iff all components are equal. Sparseness of a matrix is the mean sparseness of its column vectors.

The configuration of this example is sparse data matrix with Standard NMF - Divergence factorization method using Random Vcol algorithm for initialization and rank 15 (the number of hidden topics).

Because of nonnegativity constraints, NMF has impressive benefits in terms of interpretation of its factors. In text processing applications, factorization rank can be considered the number of hidden topics present in the document collection. The basis matrix becomes a term-by-topic matrix whose columns are the basis vectors. Similar interpretation holds for the other factor, mixture matrix. Mixture matrix is a topic-by-document matrix with sparse nonnegative columns. Element j of column 1 of mixture matrix measures the strength to which topic j appears in document 1.

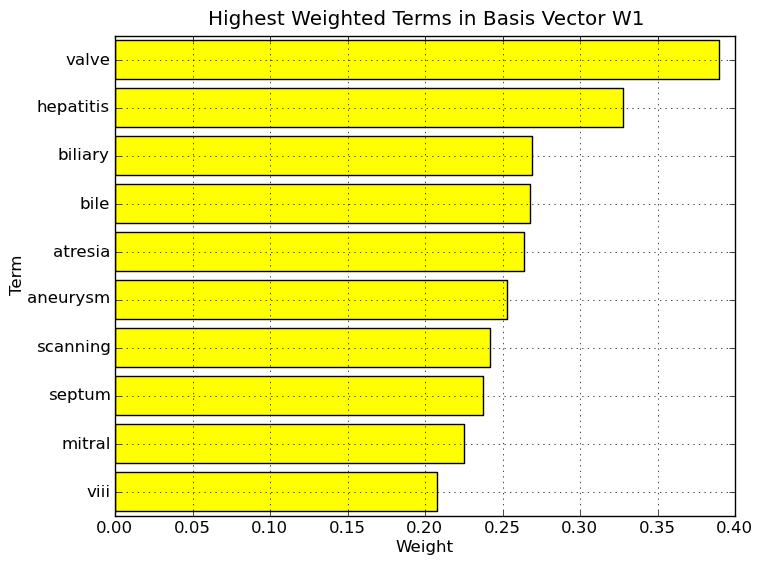
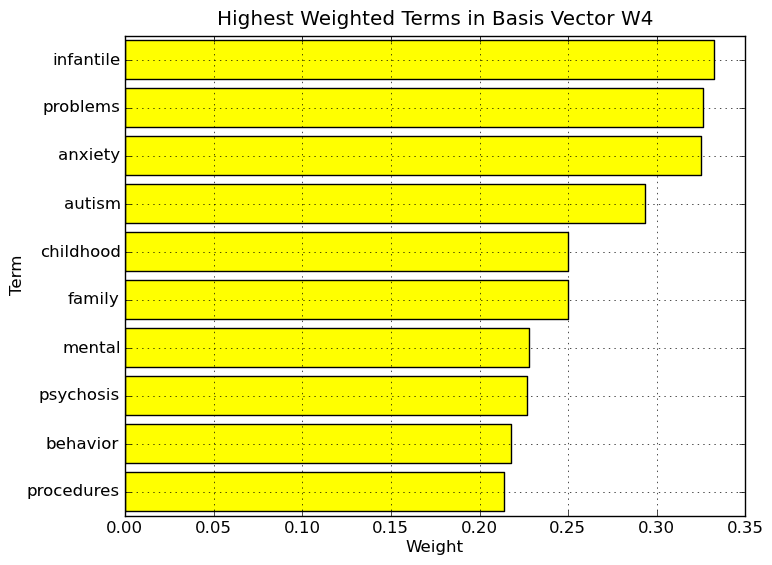
Interpretation of NMF - Divergence basis vectors on Medlars data set. Highest weighted terms in basis vector W1. The nonzero elements of column 1 of W (W1), which is sparse and nonnegative, correspond to particular terms. By considering the highest weighted terms in this vector, we can assign a label or topic to basis vector W1. As the NMF allows user the ability to interpret the basis vectors, a user might attach the label liver to basis vector W1. As a note, the term in 10th place, viii, is not a Roman numeral but instead Factor viii, an essential blood clotting factor also known as anti-hemophilic factor. It has been found to be synthesized and released into the bloodstream by the vascular, glomerular and tubular endothelium and the sinusoidal cells of the liver.

Interpretation of NMF basis vectors on Medlars data set. Highest weighted terms in basis vector W4.

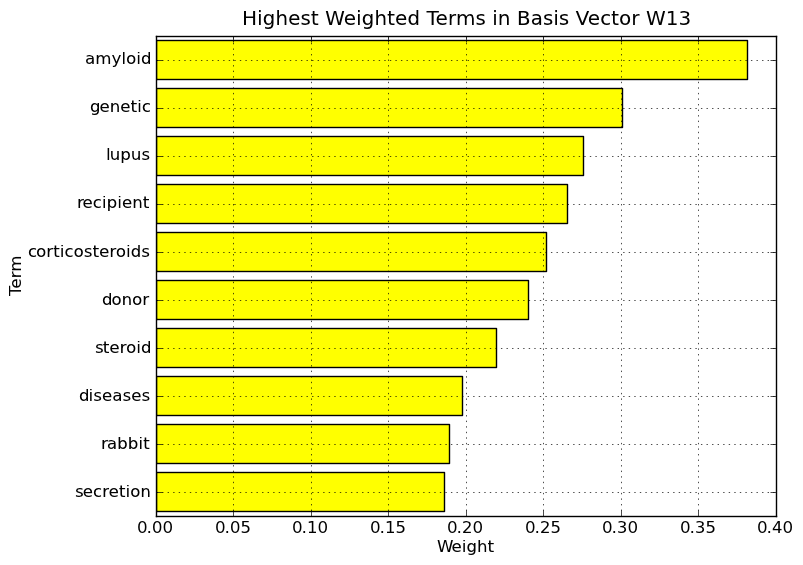
Interpretation of NMF basis vectors on Medlars data set. Highest weighted terms in basis vector W13.

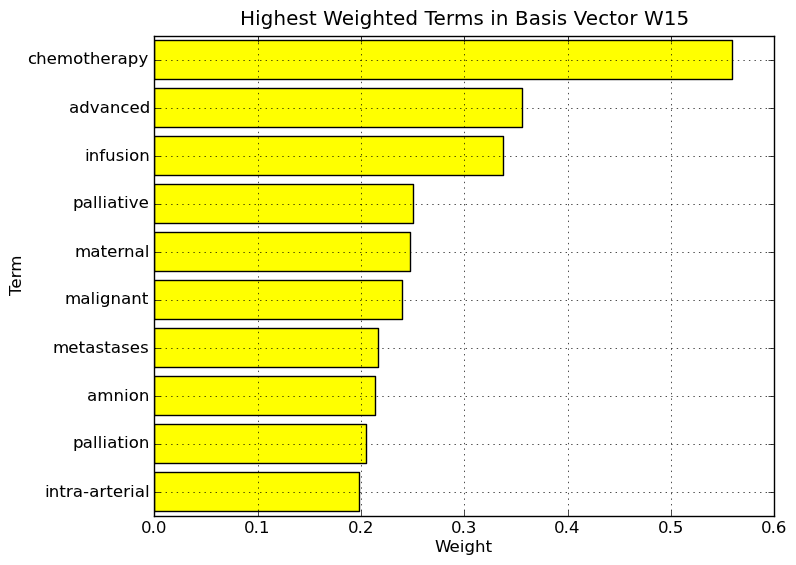
Interpretation of NMF basis vectors on Medlars data set. Highest weighted terms in basis vector W15.

To run the example simply type:

python documents.py

or call the module’s function:

import nimfa.examples
nimfa.examples.documents.run()

Note

This example uses matplotlib library for producing visual interpretation of NMF basis vectors on Medlars data set.

nimfa.examples.documents.factorize(V)

Perform NMF - Divergence factorization on the sparse Medlars data matrix.

Return basis and mixture matrices of the fitted factorization model.

Parameters:V (scipy.sparse.csr_matrix) – The Medlars data matrix.

nimfa.examples.documents.plot(W, idx2term)

Plot the interpretation of NMF basis vectors on Medlars data set.

Parameters:

• W (scipy.sparse.csr_matrix) – Basis matrix of the fitted factorization model.
• idx2term (dict) – Index-to-term translator.

nimfa.examples.documents.preprocess(V, term2idx, idx2term)

Preprocess Medlars data matrix. Remove stop words, digits, too short words, words that appear 2 times or less in the corpus and words that appear 50 times or more.

Return preprocessed term-by-document sparse matrix in CSR format. Returned matrix’s shape is 4765 (terms) x 1033 (documents). The sparse data matrix is converted to CSR format for fast arithmetic and matrix vector operations. Return updated index-to-term and term-to-index translators.

Parameters:

• V (scipy.sparse.lil_matrix) – The Medlars data matrix.
• term2idx (dict) – Term-to-index translator.
• idx2term (dict) – Index-to-term translator.

nimfa.examples.documents.read()

Read medical abstracts data from Medlars data set.

Construct a term-by-document matrix. This matrix is sparse, therefore scipy.sparse format is used. For construction LIL sparse format is used, which is an efficient structure for constructing sparse matrices incrementally.

Return the Medlars sparse data matrix in LIL format, term-to-index dict translator and index-to-term dict translator.

nimfa.examples.documents.run()

Run NMF - Divergence on the Medlars data set.